製造業の生産性向上を進めるなら
まず生産計画の精度の向上を
考慮に入れる必要があります
でもそのまえにお客様からの注文が
どのようにやってくるのか
需要予測がとても大切です
でもその需要予測の手法には
どのようなものがあるのか？
ご存じない方も多いとのことで
需要予測手法について情報を
整理してみることにしました
今回も読み終えるまでの時間
しばらくお付き合いください
需要予測の２つの方向性
需要予測を進めるには以下の
大きく２つの方向性があります
方向性２：統計的計算による予測
方向性１：ヒトの感覚による予測
取引先の方向性や営業情報
季節的な変動や市場動向など
考えるべきことは結構多くあります
ただの勘だけに頼ることは危険だと
考える方もいらっしゃるかもですが
実はこの人間の勘というものは
結構優秀なんですよ
なので次の統計的計算の手法を
組み合わせて予測することが
結構重要になってくるんですよね
２：統計的計算による予測
これには使える手法が３つあります
次の章で詳しく説明していきます
需要予測に使える３つの統計的手法
需要予測には統計的手法として
以下の３つが代表的です
手法２：指数平滑法
手法３：回帰分析法
それぞれもう少しだけ
補足を進めてみましょう
手法１：移動平均法
平均法は皆さまご存じかと思います
過去実績の平均を計算することで
需要予測として採用するのは
通常、最初に思いつく予測手法です
この移動平均法というのは
平均を移動型で計算する手法です
たとえば対象範囲を６か月とすれば
過去６か月分の平均を計算します
意図はもっとも近い６か月だけを
参考にする計算の方が
精度が高いだろうとする考え方です
移動平均法の計算例
移動平均法の計算例
4月の予測値
予測値 ＝ (32+27+36+44+48+50)/6
＝ 39.5 ≒ 40
5月の予測値
予測値 ＝ (27+36+44+48+50+40)/6
＝ 40.8 ≒ 41
たとえば上記の計算例をご覧下さい
今期の４月の予測値を計算するのに
昨年度の実績値を参考にします
次数：６か月と設定した場合
過去の実績値、具体的には昨年度の
10月、11月、12月、1月、2月、3月の
平均を求めることで予測値とします
同様に５月の予測値を計算するのに
11月、12月、1月、2月、3月、4月の
平均を求めることで予測値とします
さらに『近さ』を重視するため手法
加重移動平均法というのもあります
加重移動平均法の計算例
加重移動平均法の計算例
4月の予測値
予測値 ＝ (0.1*36+0.2*44+0.3*48+0.4*50)
＝ 46.7 ≒ 47
5月の予測値
予測値 ＝ (0.1*44+0.2*48+0.3*50+0.4*47)
＝ 47.8 ≒ 48
今期の４月の予測値を計算するのに
昨年度の実績値を参考にしますが
次数：４か月として重みづけを
掛け算して算定する手法です
具体的には過去の実績値の
12月、1月、2月、3月を参考にし
もっとも近い3月実績に０．４を
次に近い2月実績に０．３を
次に近い1月実績に０．２を
最も遠い12月実績に０．１を掛けて
より近い方に重みをつけて
平均を求めることで予測値とします
４つの実績に掛けてる指数の合計が
１になっているのて自然と平均に
なっているわけですよね
同様に５月の予測値を計算するのに
1月、2月、3月、4月を参考にし
もっとも近い4月実績に０．４を
次に近い3月実績に０．３を
次に近い2月実績に０．２を
最も遠い1月実績に０．１を掛けて
予測値を計算します
この『近さ』を重視する考え方を
さらに重視する計算手法に
指数平滑法という手法があります
手法２：指数平滑法
指数平滑法とは２つの情報を
組み合わせて予測値を計算します
具体的には過去の予測値と実績値
計算式は以下のとおり
予測値＝a×前回実績値＋（1-a）×前回予測値
（ａ：平滑定数）
aが1に近くなるほどより新しい
実績データを重視した予測ができ
0に近くなるほど
過去データを重視した計算になります
この計算方法は重みａを
指数関数的に変化させていくことに
大きな特徴があります
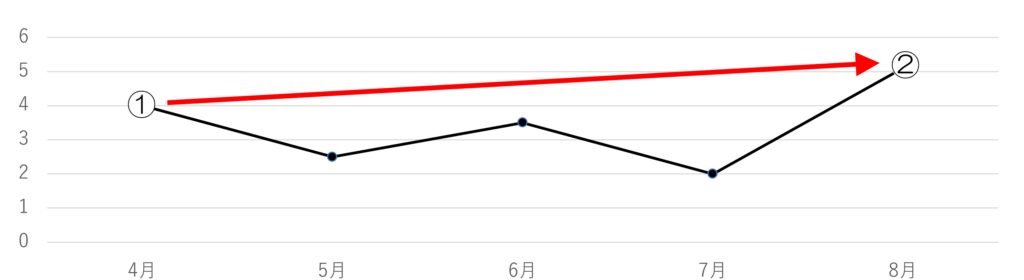
手法３：回帰分析法
回帰分析法イメージ
上記に示した実績の推移①→②を
ｙ＝ａx × ｂ等の数式に置き換えて
将来の需要を予測する手法が
この回帰分析法です
説明したい変数yを目的変数
それを予測するための変数xを
説明変数とよびます
説明変数が１つの場合を短回帰分析
複数の場合を重回帰分析と言います
現在ではビッグデータ分野で
多様されている手法でもあるので
改めて深く学習をしてみても
いいのかも知れませんね
まとめ
需要予測はそれぞれの業界や
主要取引先の状況によって
適した手法や情報収集範囲が
変わってくるものです
なのでこればかりは最適な手法を
探り当てるしかないのが現状です
つまり何ごとも仮説→検証で
実際に試して見つけていくのが
もっとも効率的な方向性であり
ここから逃げていては始まりません
ぜひ自社の環境に最適な
需要予測の手法を確立してください
それでは今日はここまでです
今後とも宜しくお付き合い下さい☆
長文乱文を最後まで読んでくださり
いつもありがとうございます♪
すべては御社の発展のために
すべてはあなたの笑顔のために
