新QC7つ道具の紹介シリーズ6つ目は
アローダイヤグラム法の書き方です
アローダイヤグラム法は
シスアドなど情報管理系や
中小企業診断士などの資格で
取り扱われている有名な手法です
さすがに新QC7つ道具にも
カウントされているほど
とっても便利な手法なんですよねー
今回はその資格系の例題を
作成手順ごとに解き方を解説して
理解を深めていくことにしましょう
ついでに資格獲得もご検討ください
では早速内容に入っていきましょう
アローダイヤグラム法とはなにか?
まずはアローダイヤグラム法とは?
いつものように辞書を調べてみます
アローダイヤグラム法(読み方)あろーだいやぐらむほう
新QC7つ道具のひとつで、パート図、矢線図、日程計画図とも呼ばれる。ある作業の内容と日程の流れを、矢印で順に追って表した図式のこと。アローダイヤグラムは、複雑な工程や細かい時間配分を図式化できるため、大規模なプロジェクトの作業の進行状況を的確に把握したい場合に利用される。
出典 デジタル用語辞典/ASCII.jp より
複数な作業が複雑に込み入っている
日程計画を作成しようとする時
アローダイヤグラム:矢線図を使い
効率的な最短ルートを見つけます
英語ではArrow diagram method
当たり前ですがそのままです、笑
アローダイヤグラムのイメージ図
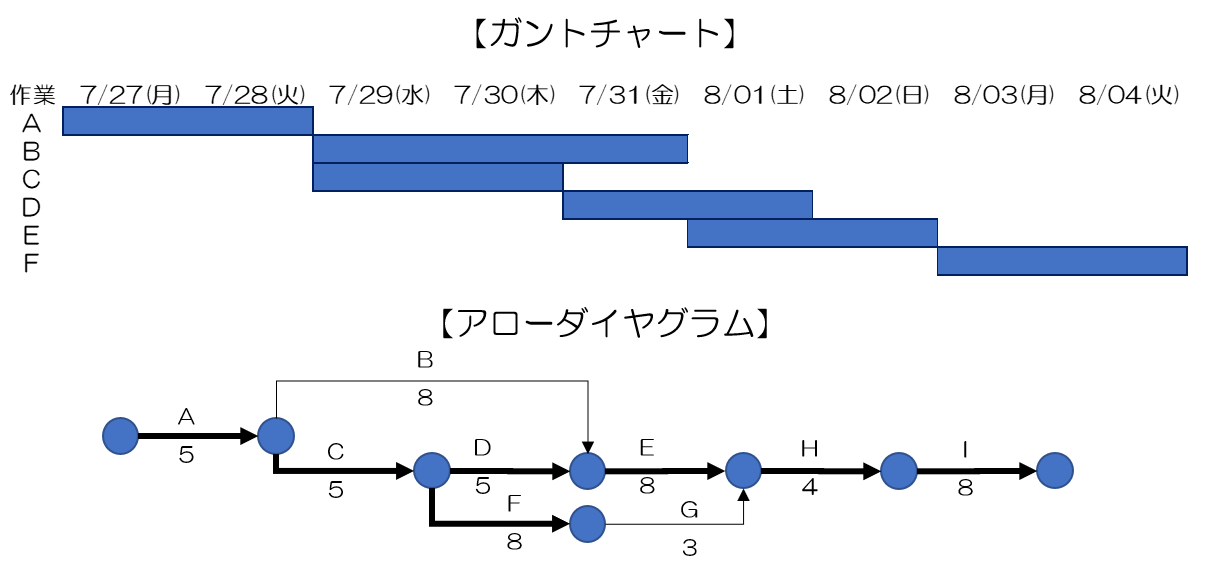
アローダイヤグラム法のイメージ図
そもそも日程管理の手法としては
ガントチャートと呼ばれる手法が
今も一般的に使われています
横軸に日付、縦軸に必要作業を並べ
作業ごとにスケジュールを記す方法
がガントチャートです
(注:正確にはバーチャート方式)
これって、よく使われてますよね
でもこのガントチャートって
単純な作業過程の場合は便利ですが
複雑に絡み合っている仕事の場合は
なんとも管理がし辛くなってきます
そんな代替え手法としてこの
アローダイヤグラム法が活躍します
アローダイヤグラム法の特徴
アローダイヤグラムでは
作業のスタートからゴールまで
矢印でつながっているので
各作業の相互関係や順序が
わかりやすくなっています
また図の書いてある数字は
作業のかかる日数を表しているので
合算するとどれくらいかかるのか
イメージどおり確認できます
ガントチャートよりは作成に
時間がかかることが弱点ですが
それを覗けば結構使えそうですね!
アローダイヤグラムの構成要素
アローダイアグラムでは
作業を矢印の線で表します
この線をアクティビティと呼び
結合点である丸をノードと呼びます
また、スタートからゴールまでに
複数のルートを書くことが多いが
その中で最も時間のかかるルートを
太字=クリティカルパスと呼びます
作業の遅れが許されないため
『最も注視すべきルート』という
わけですよね
アローダイヤグラム法の活用例
アローダイヤグラム法がもっとも
活用されるのは少し応用を加えた
PERTと呼ばれる手法です
PERTとは
Program Evaluation and Review Technique
を略したもので
複数の作業で構成されるプロジェクトを
効率的に実行するためのスケジュールを
作成する手法であるのですが。。。
アローダイヤグラム法に
最早着手日と最遅着手日の2情報を加え
より管理しやすくしたものです
このツールを理解するために
まずは作業手順を確認します
アローダイヤグラム法の書き方ステップ
アローダイヤグラムの書き方は
以下の4ステップで説明します
[STEP2]アローダイヤグラムの作図
[STEP3]最早着手日と最遅着手日の記入
[STEP4]クリティカルパスの確認
ではこれらについて簡単に
説明してきましょう
[STEP1]必要な作業の洗い出しと調査
まずは必要な作業を洗い出して
その作業日数と構造を調査して
準備を進めます
[STEP2]アローダイヤグラムの作図
作業を1つずつ日数と構造を
確認しながらノード間を矢印で
つなぎながら記入していきます
[STEP3]最早着手日と最遅着手日の記入
全体構造が完成したら各ノードに
最早着手日と最遅着手日を記入して
その最適化を図っていきます
[STEP4]クリティカルパスの確認
最後に最も時間のかかるルートを
太字で線を引きなおして
クリティカルパスをわかりやすく
示します
これでアローダイヤグラムは
完成するのですが
言葉で説明されてもちょっと
イメージしにくいですよね
ま、習うより慣れろなツールなので
例題の解き方を解説しましょう
例題の解き方を作成手順ごとに解説
まずは例題はとして
平成30年の中小企業診断士試験で
出題された以下の問題の解き方を
解説させていただきます
下表に示される作業A〜Fで構成されるプロジェクトについて、PERT を用い て日程管理をすることに関する記述として、最も適切なものを下記の解答群から選べ。
作業 作業日数 先行作業 A 3 なし B 4 なし C 3 A D 2 A E 3 B , C , D F 3 D 〔解答群〕
ア このプロジェクトのアローダイアグラムを作成するには、ダミーが2本必要である。
イ このプロジェクトの所要日数は8日である。
ウ このプロジェクトの所要日数を1日縮めるためには、作業Fを1日短縮すれ ばよい。
エ 作業Eを最も早く始められるのは6日後である。
出典 中小企業診断士試験 運営管理 平成30年度 第6問 より
[STEP1]必要な作業の洗い出しと調査
例題ではもうすでに整理されて
条件が出ていますので
それを確認します
実際にはこの表をつくることが
1つ目のステップというわけです
では次のステップに移りましょう
[STEP2]アローダイヤグラムの作図
作業を1つずつ日数と構造を
確認しながらノード間を矢印で
つなぎながら記入していきます
詳しくは次のとおりです
作業Aを作図する
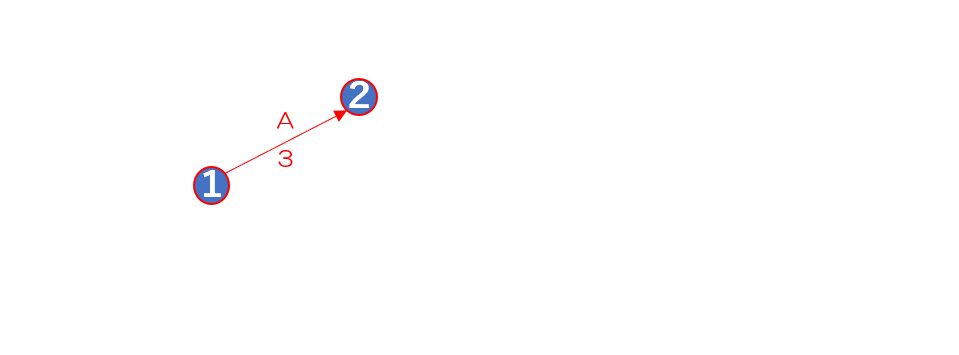
アローダイヤグラム法 作業A
最初に作業Aのアクティビティを
作図していきます
作業Aは先行作業がないため
1のノードから2のノードへ
矢印を書いてアクティビティを示し
作業名と作業日数を書き込みます
作業Bを作図する
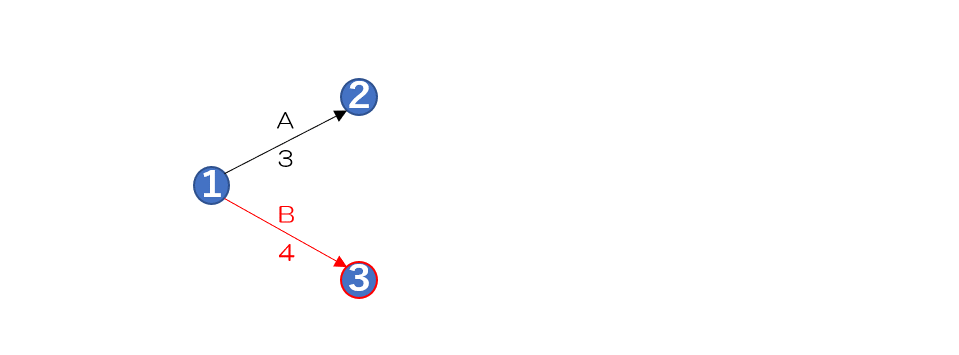
アローダイヤグラム法 作業B
次に作業Bのアクティビティを
作図していきます
作業Bも先行作業がないため
1のノードから3のノードへ
矢印を書いてアクティビティを示し
作業名と作業日数を書き込みます
作業Cを作図する
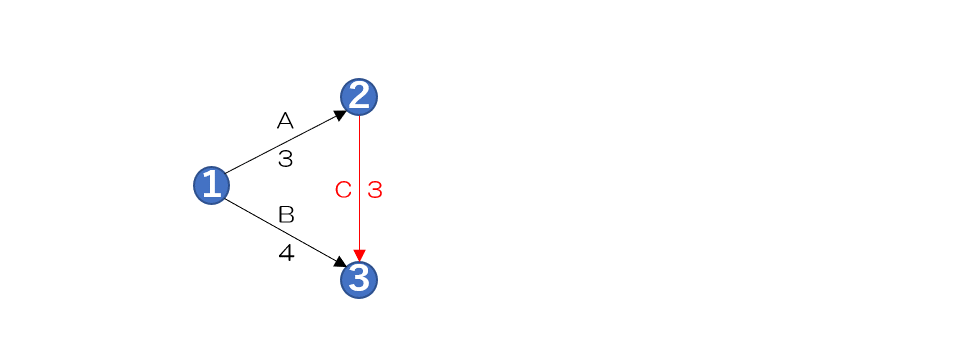
アローダイヤグラム法 作業C
次に作業Cのアクティビティを
作図していきます
作業Cは先行作業が作業A
そして作業CはEの選考作業であり
Eの先行作業はB、C、Dなので
作業Bがある3のノードへ
矢印を書いてアクティビティを示し
作業名と作業日数を書き込みます
作業Dを作図する
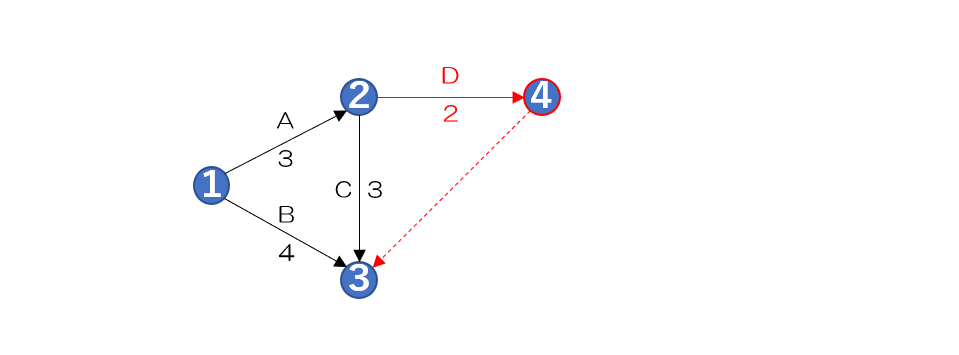
アローダイヤグラム法 作業D
次に作業Dのアクティビティを
作図していきます
作業Dの先行作業が作業A
そして作業DはE、Fの先行作業
しかも作業Fの先行作業はDだけ
そのためノード2から4のノードへ
矢印を書いてアクティビティを示し
作業名と作業日数を書き込みます
またEの先行作業でもあるため
作業BとCが集まっている3にも
ダミー線を点線で書き込みます
このように並行作業がある場合は
ダミー線を記入して表現します
ただしこのダミー作業は
実体を持たない作業なので
所要時間は0となります
作業Eを作図する
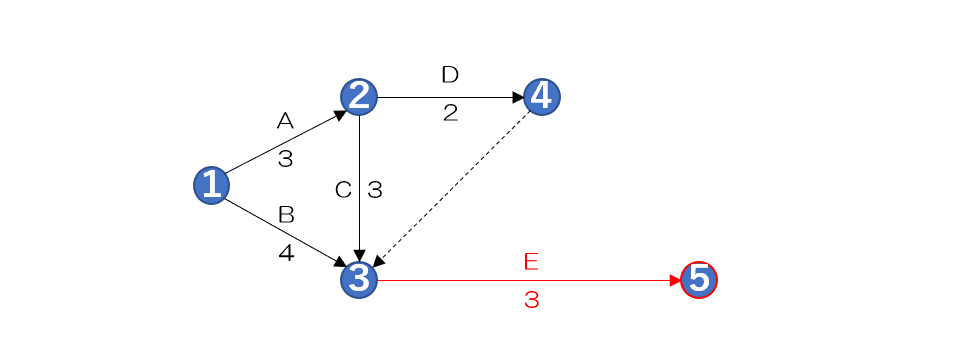
アローダイヤグラム法 作業E
次に作業Eのアクティビティを
作図していきます
作業Eは先行作業がB、C、D
そのため3のノードから新しい5へ
矢印を書いてアクティビティを示し
作業名と作業日数を書き込みます
作業Fを作図する
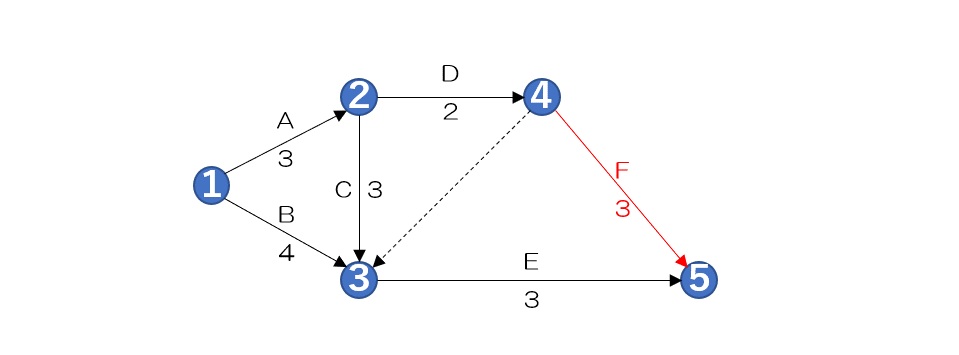
アローダイヤグラム法 作業F
最後に作業Fのアクティビティを
作図していきます
作業Fは先行作業が作業Dのため
4のノードから5のノードへ
矢印を書いてアクティビティを示し
作業名と作業日数を書き込みます
[STEP3]最早着手日と最遅着手日の記入
全体構造が完成したら各ノードに
最早着手日と最遅着手日を記入して
その最適化を図っていきます
最早着手日を記入する
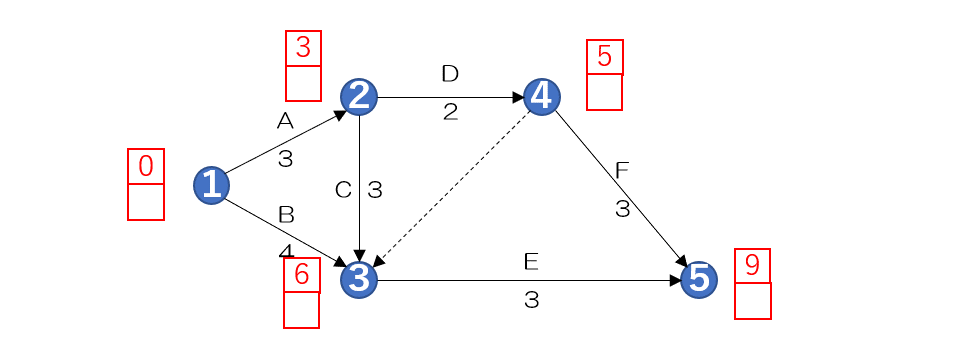
アローダイヤグラム法 最早着手日の記入
まず各ノードごとに上下のマスを
作図していきます
ノード1はスタートなので0を
上のマスに記入
ノード2は作業A以外の
アクティビティがないので
作業Aの作業日数の「3」を記入
ノード3はB、C、D(ダミー)が
集まっているのでもっとも日数が
かかる経路を積算して記入します
つまりA→Cなので「6」です
ノード4は作業D以外はないので
ノード2の「3」に作業Dの2を
加算して「5」を記入します
ノード5は作業E、Fが集まって
いるのでそのもっとも日数が
かかる経路を積算して記入します
つまり
ノード4から伸びている作業Fより
ノード3から伸びている作業Eが
日数がかかっているので
「6」に作業Eの3日を加算して
「9」を記入します
最遅着手日を記入する
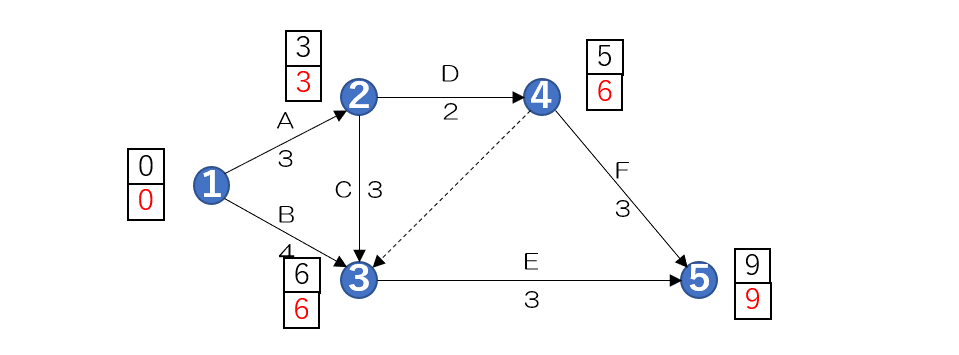
アローダイヤグラム法 最遅着手日の記入
次に最遅着手日を記入します
まず最後の最早着手日「9」を
ノード5の最遅着手日に設定して
下のマスに記入します
そこから逆算して最遅着手日を
算定していきます
具体的にはノード5の最遅着手日の
「9」から作業Fの3日を引いて
ノード4の最遅着手日を「6」とし
下のマスに記入します
さらにノード5の最遅着手日の
「9」から作業Eの3日を引いて
ノード3の最遅着手日を「6」とし
下のマスに記入します
そしてノード3の最遅着手日の
「6」から作業Cの3日を引いて
ノード2の最遅着手日を「3」とし
続いてノード2の最遅着手日の
「3」から作業Aの3日を引いて
ノード1の最遅着手日を「0」とし
それぞれ下のマスに記入します
この時ノード3の最遅着手日の
「6」から作業Bの4日を引いて
ノード1の最遅着手日を「2」とは
しません
もうおわかりですよね
A→Cルートの方が長くかかるので
そちらを優先しているわけです
結局、間に合わないと
意味がありませんものね
[STEP4]クリティカルパスの確認

アローダイヤグラム法 クリティカルパス
そして最後に
最早着手日と最遅着手日が
同じになるノードをつないでみると
クリティカルパスが明らかになると
いうわけです
ここは他の矢印と区別するため
太線にしておきます
この例題の答え
ア.このプロジェクトのアローダイアグラムを作成するにはダミーが2本必要である。
ダミー線はノード4→ノード3の
1本だけとなりましたよね!
これでアの選択肢は消えました
イ.このプロジェクトの所要日数は8日である。
ノード5の最遅着手日は
「9」ですよね
なのでこの選択肢もなし
ウ.このプロジェクトの所要日数を1日縮めるためには、作業Fを1日短縮すれ ばよい。
このプロジェクトの所要日数の
短縮を検討していくためには
クリティカルパスが示すプロセスを
短くしていく必要があります
つまり現在のクリティカルパスは
ノード1→2→3→5であるため
作業A→作業C→作業Eが関係します
つまり作業Fを短縮しても
クリティカルパスは変わらない
なのでこの選択肢もありえません
エ.作業Eを最も早く始められるのは6日後である。
最も早く始められる日は
最早着手日で確認をしていきます
作業Eのアクティビティの元は
ノード3ですよね
そのノード3の最早着手日は
「6」となっています
そのためこの選択肢が正解です
いかがでしょう?
だいぶ理解いただけたでしょうか?
今回のまとめ
さて、今回は新QC7つ道具として
アローダイヤグラムを紹介しました
これも慣れてしまうと
本当に便利なツールとなります
こういった図を使いこなすと
多くの方々と情報共有が進みます
やはり全員のレベルが組織のレベル
少しずつ高め合って
いきたいものですね
それでは今日はここまでです
今後とも宜しくお付き合い下さい☆
長文乱文を最後まで読んでくださり
いつもありがとうございます♪
すべては御社の発展のために
すべてはあなたの笑顔のために