新QC7つ道具の使い方シリーズの
最後を飾るのはもっとも難しい
マトリックスデータ解析法です
このツールは正直、
統計学を詳しく学ぶ必要があるため
その関連知識がない方にとっては
どうやって使えばよいかわかりません
ですが新QC7つ道具を考えた方が
わざわざのこのグループに入れた
その意図をくみ取るとすると
やはりどんなものかは知っておく
必要があると思います
そのため今回のお役立ち情報は
このマトリックスデータ解析法は
どんなツールで、何の役に立つのか
それを説明していければと思います
マトリックスデータ解析法とはなにか?
マトリックスデータ解析法とは?
いつものようにまずは
辞書を確認してみましょう
マトリックスデータ解析法(読み方)まとりっくすでーたかいせきほう
新QC7つ道具のひとつ。項目間の特性や関連性などを数値データで表し、分析するための方法。表をもとに散布図などを作成し、数値データを視覚的に表して関連性や傾向を分析する。
出典 デジタル用語辞典/ASCII.jp より
簡単に書いてあるので
わかりやすいですね!
ただし簡単すぎて何を言っているか
わからないのが正直なところ、笑
実はマトリックスデータ解析法とは
整理したマトリックスデータを
ある統計手法を使って分析して
最終的にグラフ化することで
新たな関連性や傾向を見える化する
方法なんです
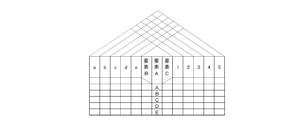
このマトリックスデータとは
主にL型マトリックス図で
整理したデータのことを指します
では早速ではありますが
マトリックスデータ解析を
どう進めるのか説明することで
どんなものか理解を深めましょう
マトリックスデータ解析法の使い方
マトリックスデータ解析の
使い方ステップは以下のとおり
[STEP2]統計手法を駆使して分析
[STEP3]分析結果をグラフで表現
[STEP4]グラフを観察して結論づける
ではもうすこしだけ詳しく
説明を加えていきましょう!
[STEP1]分析するデータを準備
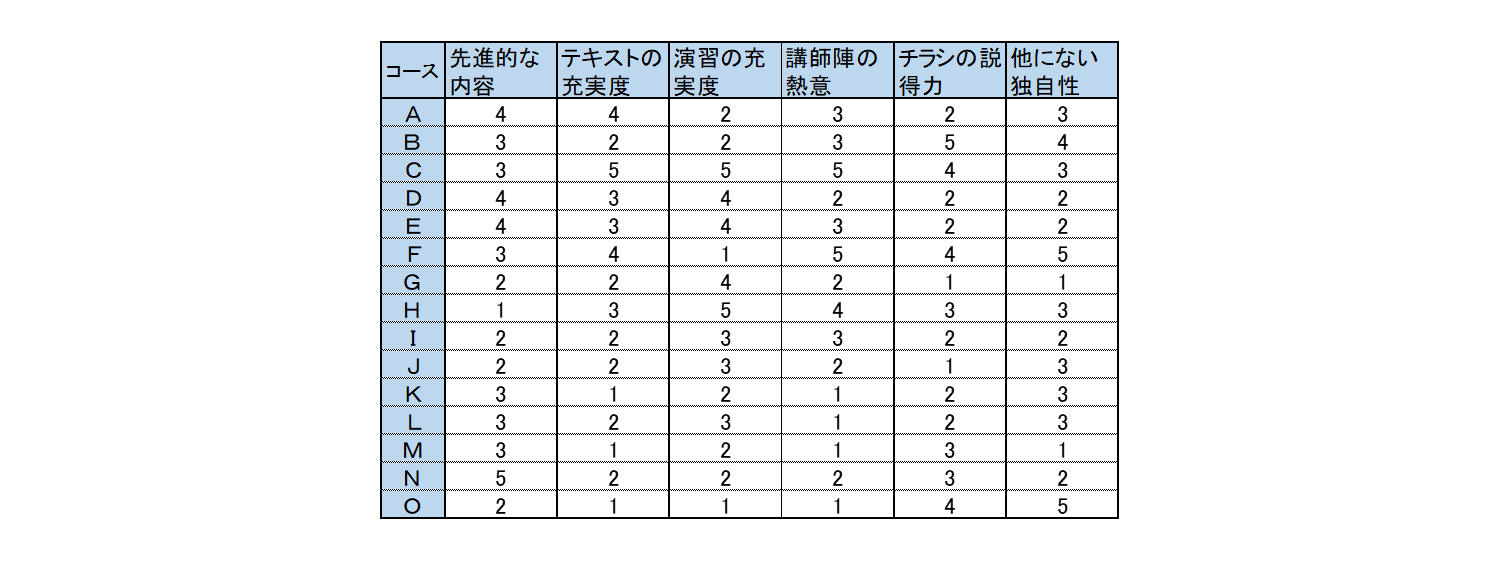
マトリックスデータ解析法に使うL型マトリックス図
まずは分析するデータを準備します
たとえば
セミナーや研修などの評価項目を
コースごとに5段階評価した
データがあったとします
これらから新たな関連性や傾向を
つかむことを目的に進めます
[STEP2]統計手法を駆使して分析
このマトリックスデータ分析法では
統計手法である多変量分析
その中でも主成分分析という
手法を使って分析していきます
つまりたくさんの変数があったときに
それぞれがどんな関連性があるのか
それを2~3個の項目に置き換えて
解釈しやすくする分析方法を使います
これを詳しく説明すると統計学の本が
書けるほど難解のため簡略化するが
その多くはエクセルのアドイン機能や
関数で計算できるようになっています
そんな主成分分析とはどんな分析か
ちょっとだけ紹介してみますので
そんなものか、とご理解ください、笑
①評価項目ごとに基準化する
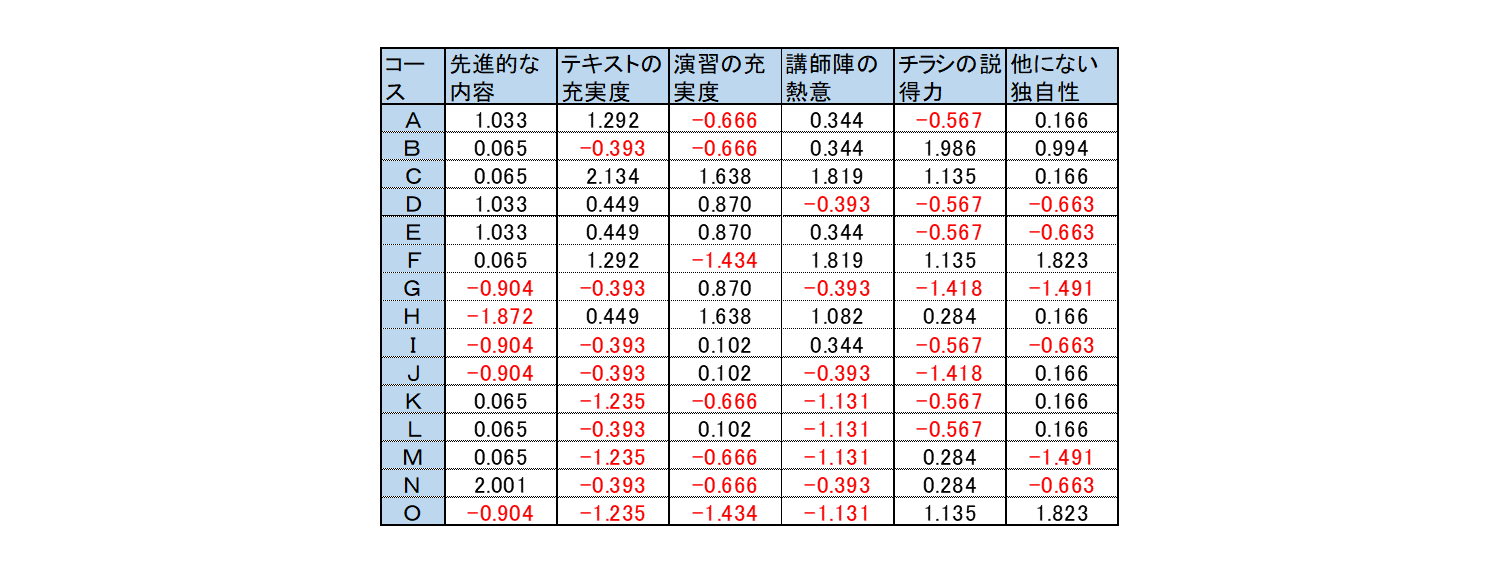
基準化したデータ
まず最初のステップは
そのままの数値では比較できないため
平均値を引き算して標準偏差で割って
比較できる数値に置き換えます
これを基準化を言います
②相関係数を確認する
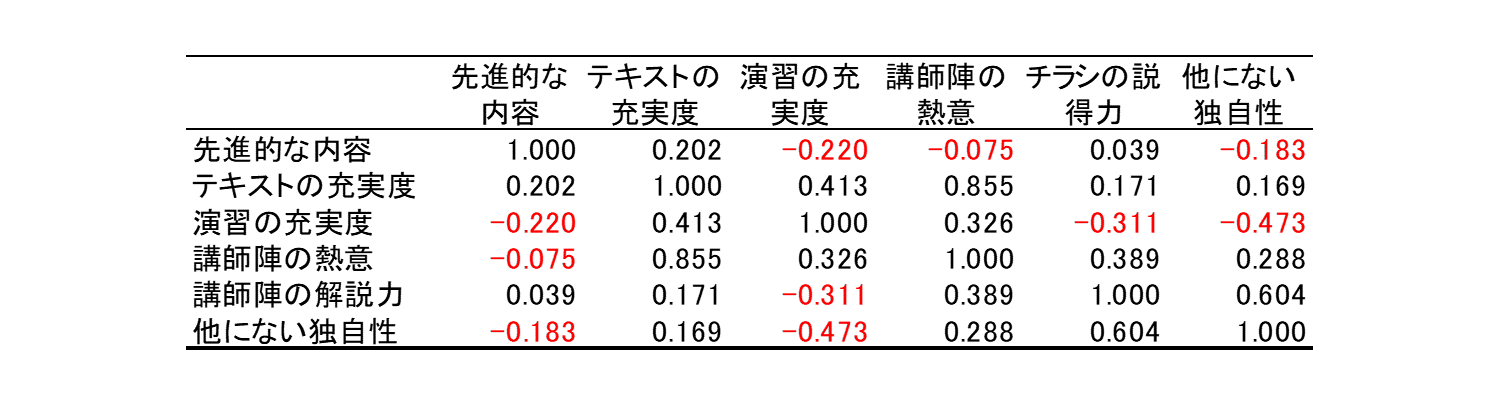
評価項目の相関係数図
基準化したデータをもとに
今回の評価項目それぞれの
相関係数を算定してみることで
その関連性を確認しておきます
1に近いほど関係性が強いことを
意味しています
逆に0に近いほど関係がない
-1は反対の関係性ですね
上図の場合は
「講師陣の熱意」と
「テキストの充実度」の相関係数が
1に近い数値:0.855であることから
強い正の相関関係があると言えます
③主成分分析を実施
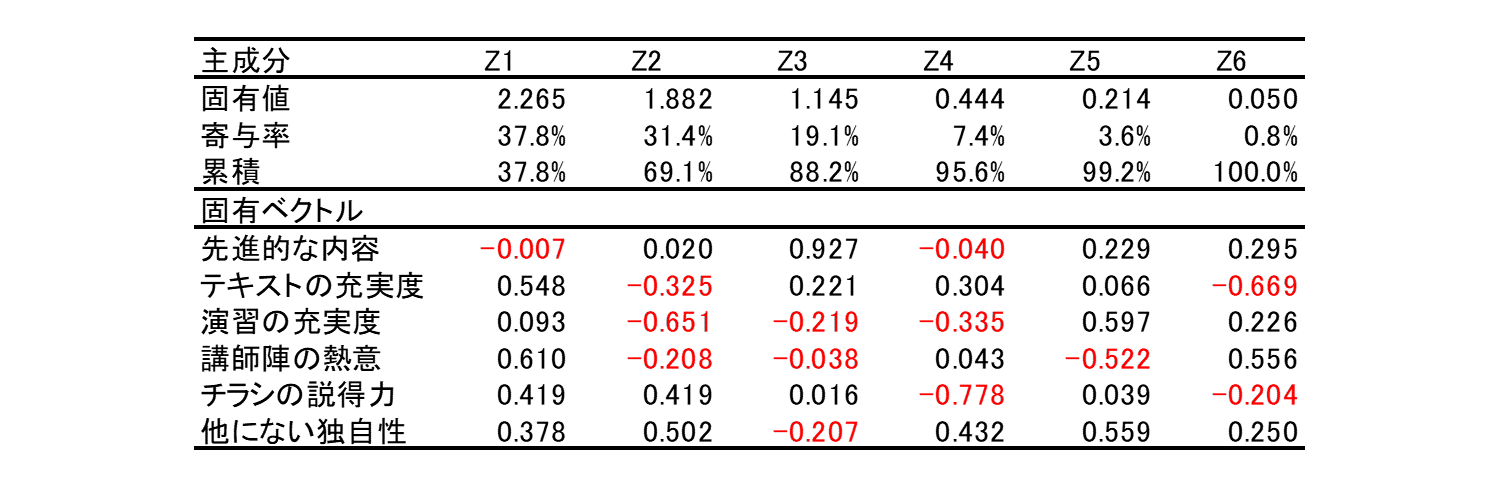
多変量解析法の主成分分析の結果
多変量解析の主成分分析を実施して
固有値、寄与率、固有ベクトルを
算定します
主成分分析によって
複数の主成分が出てきます
固有値は情報のバラツキの大きさ
寄与率はその占有率
固有ベクトルは評価項目との関係性
を表します
上図では2つの主成分で69.1%
つまり全体の約7割のバラツキを
2つの主成分で網羅していると
いうことがわかります
だったらそれをグラフ化して
見てみれば何か見つかるかも?
ってことになるわけです
④最後に主成分負荷量を算定する
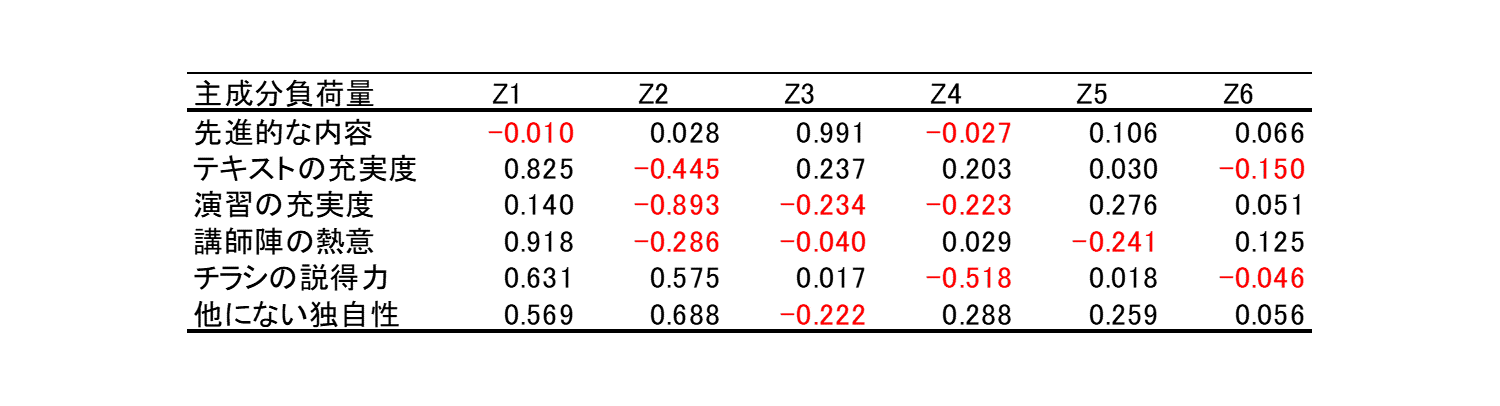
主成分負荷量の計算
固有ベクトルをグラフ化するより
もう1段、比較しやすくするため
主成分負荷量を計算します
主成分負荷量とは固有ベクトルを
相関係数化した数値を指します
詳しくは固有ベクトル値に
固有値の平方根を掛け算したものです
ではこの主成分負荷量が計算できたら
いよいよグラフ化していきます
[STEP3]分析結果をグラフで表現
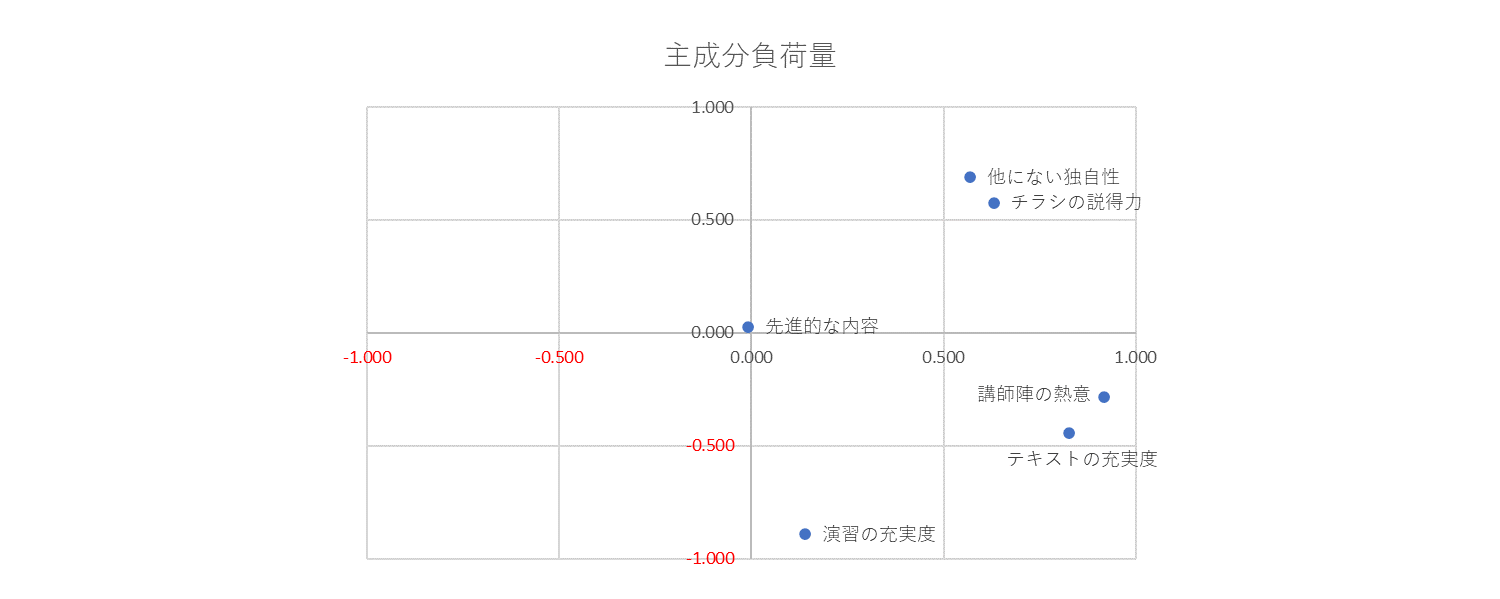
2つの主成分の相関図
主成分は6つあるのですが
全体の約7割を表現できる
2つの主成分の主成分負荷量で
相関図=グラフ化してみます
そして
その主成分は何を意味するか?を
主成分負荷量の数値で相関をみて
あたりをつけてネーミングします
Z1はほとんどがプラス方向のため
『研修・セミナー内容の出来栄え』
Z2は
「テキストの充実度」「演習の充実度」
「講師陣の熱意」がマイナスで
「先進的な内容」「チラシの説得力」
「他にない独自性」がプラスなので
『研修・セミナーの事前期待値』とでも
仮に名前をつけておきましょう
そうしながら2つの主成分の
新たな関連性や傾向を探るわけです
[STEP4]グラフを観察して結論づける
今回の例からは
主成分の2つの軸
『研修・セミナー内容の出来栄え』
と『研修・セミナーの事前期待値』が
評価を7割がた決定づける
要素であるとの結論が出たわけです
面白いですよね
この後、主成分分析では
各コースごとに主成分得点を計算し
それぞれ主成分で評価をすることで
対策を検討するなどします
今回のまとめ
さて、今回は完全に解釈することは
難しかった概念だとは思いますが
おおよそどんなことに使われるかは
ご理解いただけたかと思います
新QC7つ道具の中で唯一
難解を極める統計ツールですが
たぶんマトリックスデータ解析法を
多くのヒトが興味をもって学習して
問題解決につなげてほしいとの
想いがあったんだと想像します
たしかに新QC7つ道具に入れてれば
こうやって説明する機会もできます
こうやって大いなる先輩達の知恵を
受け取って次の世代にもしっかりと
伝えていける立場にならなければと
背筋を伸ばすきっかけとなります
皆さまはどう受けてめて
いただいたでしょうか?
さてこういったQC7つ道具
新QC7つ道具なども含めて
製造現場で応用されている
統計ツールは数多くあります
またそれは別の機会を設けて
大本の概念から丁寧に
説明していければと考えています
それでは今日はここまでです
今後とも宜しくお付き合い下さい☆
長文乱文を最後まで読んでくださり
いつもありがとうございます♪
すべては御社の発展のために
すべてはあなたの笑顔のために