QC7つ道具の使い方シリーズの10回目
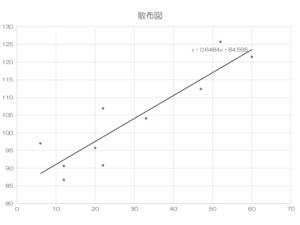
前回、散布図の作り方をお話しました
【参考記事】散布図の作り方(エクセル含む)
しかしその散布図の持つ
素晴らしい機能については
少ししか触れていませんでした
そのためこの散布図を
どのように見ていくと
どのようなことが分かるのか
見方について詳しく説明します
読み終えるまでの3分程度
お時間をお預かりします
散布図の見方(相関度合い)
相関図は2つのデータ間の関係を
調べる目的で作図しました
そのため見るべきなのはその2つの
データにどのような関係があるか?
ということに限られます
| 【相関図の6つパターン】 パターン1:ふんわりと右肩あがり パターン2:ふんわりと右肩さがり パターン3:直線的に右肩あがり パターン4:直線的に右肩さがり パターン5:カタチが分散傾向 パターン6:カタチが曲線の場合 |
ではパターン別にわかることを
順番に説明していきましょう
パターン1:ふんわりと右肩あがり
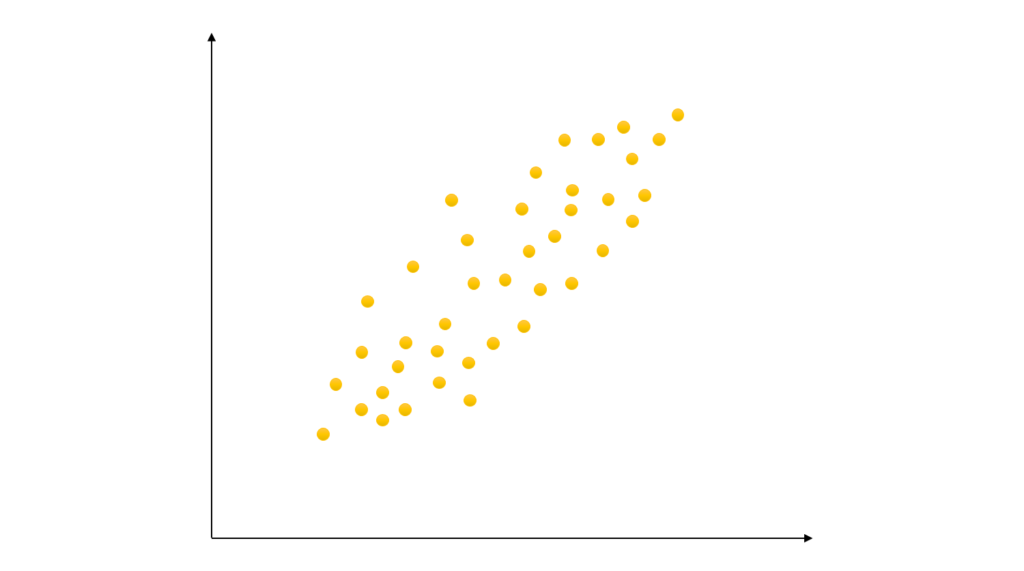
上図のように一方の変数の値が
大きくなるに従ってもう一方の変数も
大きくなっていく傾向が見える時は
この2つは『正の相関がある』と言い
2つのデータに関係性があることを
意味します
パターン2:ふんわりと右肩さがり
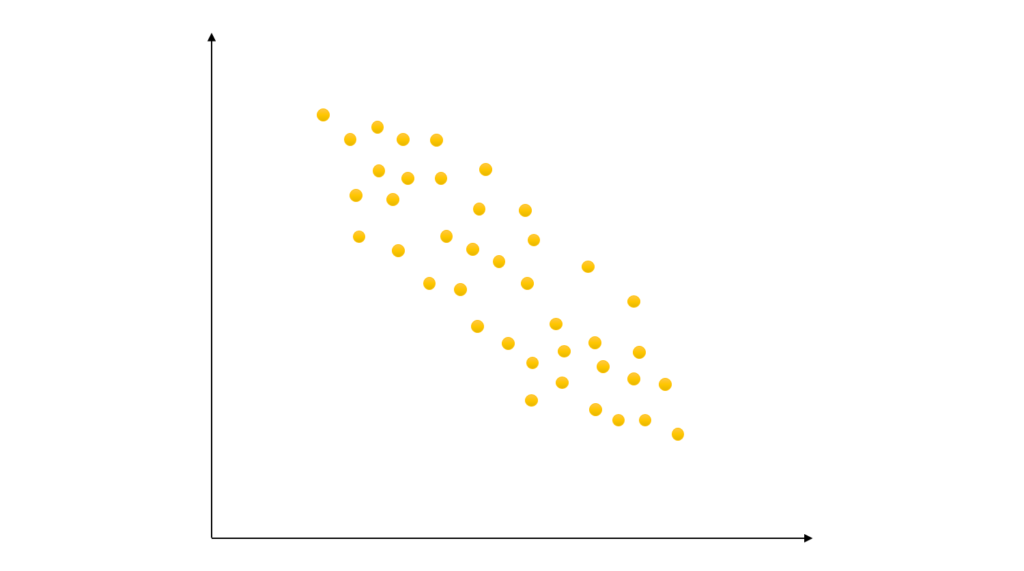
一方で反対に一方の変数の値が
大きくなるに従ってもう一方の変数が
小さくなっていく傾向が見る時は
この2つは『負の相関がある』と
言います
もちろん2つのデータの間には
関係性がある証明になり
しかもパターン1とは正反対の
反比例な関係です
パターン3:直線的に右肩あがり
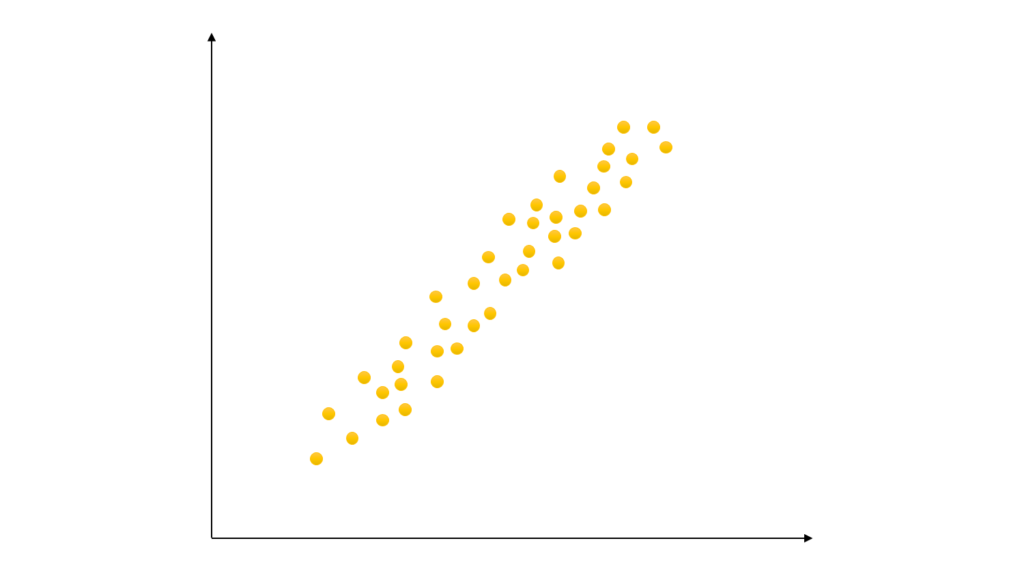
一方、こちらはパターン1にそっくり
ではありますがより直線的な集合体に
なっています
こういった直線的に点が密集すれば
より強い相関関係があることを意味し
『強い正の相関がある』と表現します
パターン4:直線的に右肩さがり
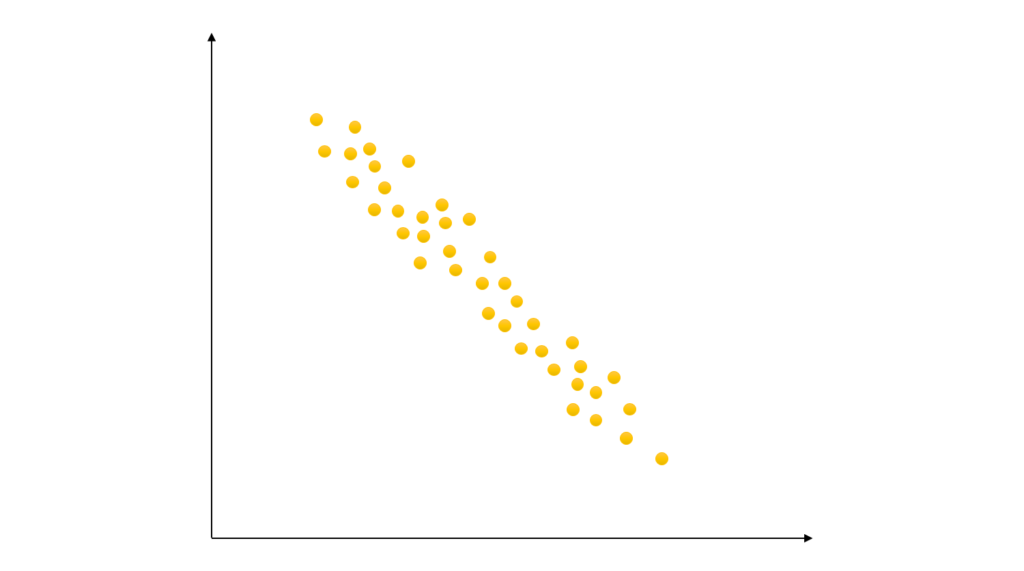
パターン3と同様にパターン2に比べ
より直線的な傾向が強いカタチです
もちろんこの場合もパターン2より
より強い相関関係があることを意味し
『強い負の相関がある』と言います
パターン5:カタチが分散傾向

上図のように一方の変数の値が
大きくなっても、もう一方の変数が
直線的な傾向が見られない場合は
この2つは『相関がない』あるいは
『無相関』と表現します
もちろん2つのデータには
関係性がありません
パターン6:カタチが曲線の場合
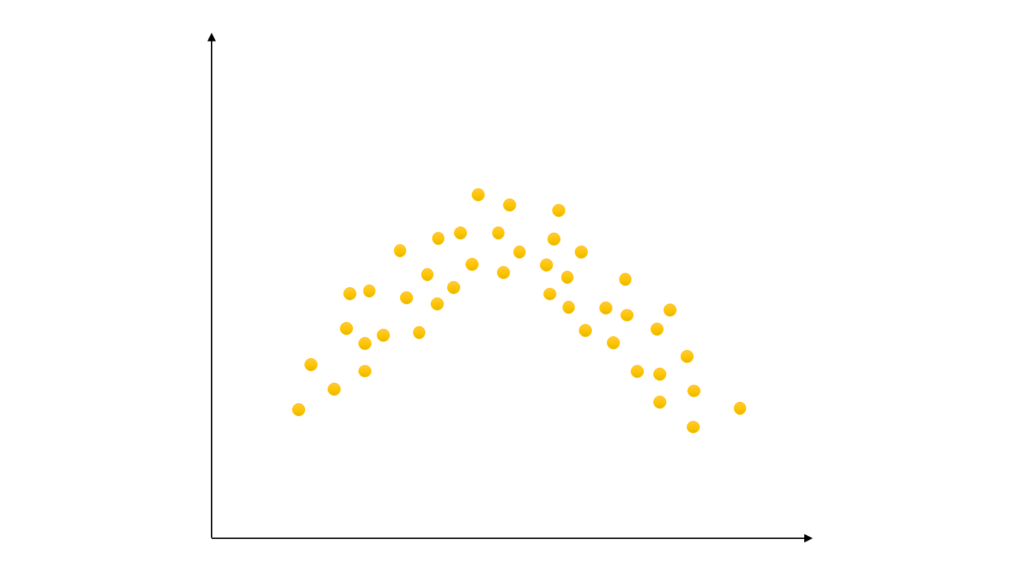
このように点が曲線になった場合
これも相関がある場合があります
この場合その2つのデータの関係を
詳しく調べて関係を突き止める必要が
あります
その他の散布図の見方(番外編)
これまで説明したきたパターンとは
違う見方をする必要があることも
あります
それは以下の3つのパターンです
| 【その他の散布図の見方(番外編)】 見方1:外れ値があった散布図 見方2:一見相関なしの散布図 見方3:偽相関が疑われる散布図 |
ここは重要ですので
もう少し詳しく解説します
見方1:外れ値があった散布図
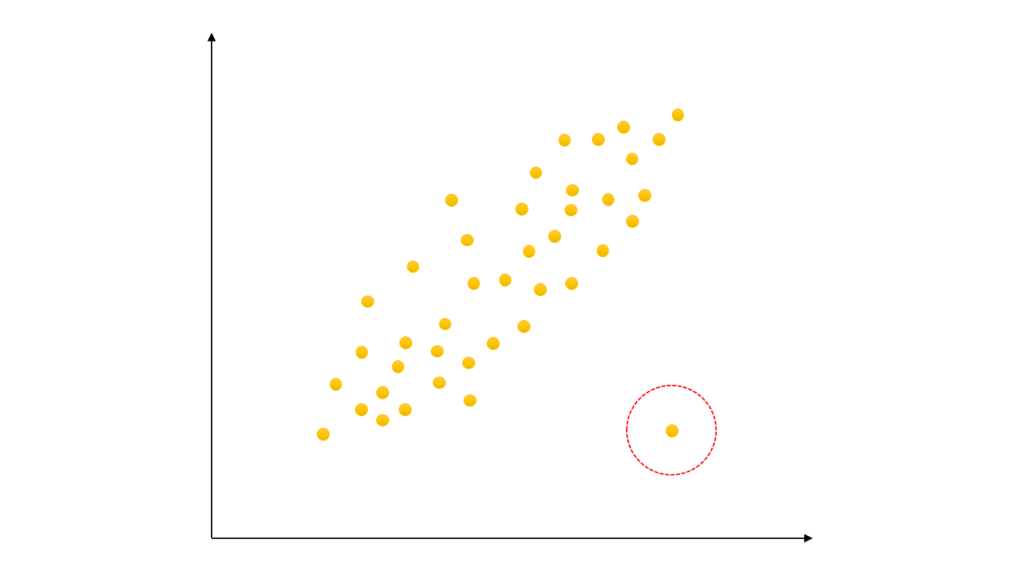
上図のように相関が見える集合から
飛び出したデータが現れることが
あります
そのようなデータを外れ値あるいは
異常値と呼びます
この外れ値はその原因を突き止めて
再発防止がとれれば散布図には
現れなくなります
しかし対策が十分でなければ
また現れるというアラームとしても
活用可能です
見方2:一見相関なしの散布図
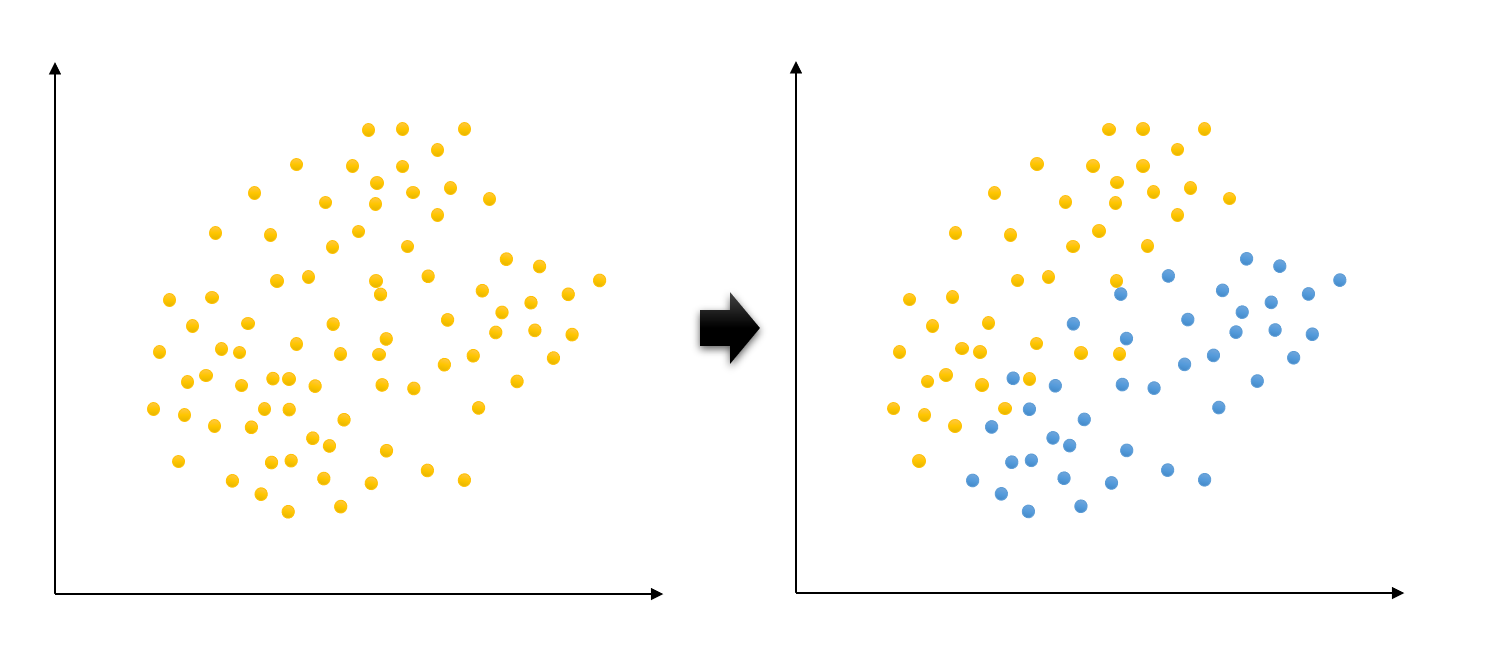
全体で見れば相関なしの見方をする
ような散布図でも、2種類の散布図に
区分け(層別)してみると
相関関係が表れます
2つのデータの関係をよく
考えてみて、想定と違う場合は
何度でも作図しなおして検証する
ことでカバーします
見方3:偽相関が疑われる散布図
これも見方2の逆のパターンで
相関関係ありそうなのに
区分けしてみるとなかった
これを『偽相関』と言います
見方2を含めてこれを見極めるには
散布図の機能を万能だと過信せず
実際のその2つのデータの関係性の
真意を想像しながら追い求める姿勢が
求められるということですね
QC7つ道具の使い方⑩散布図の見方まとめ
さて、ヒストグラムもそうですが
見方によって色んなことがわかります
これら道具を活用してあなたは
どのような課題を解決したいですか?
現実の職場と照らし合わせながら
情報を獲得し、すぐに使ってみて
役に立てて頂ければと望みます
それでは今日はここまでです
今後ともよろしくお付き合いくださいませ☆
長文・乱文を最後まで読んでくださり
いつもありがとうございます♪
すべては御社の発展のために
すべてはあなたの笑顔のために