ワークサンプリングはIE手法の中でも
とてもよく活用される分析手法です
工程内ではいったいどういった
時間の使い方がされているのか?
それを統計学を応用することで
計測者に大きな負荷をかけずに
把握することができます
でも『このやり方で本当に大丈夫?』
『ちゃんと正確に把握できているの?』
『信じられないので活用したくない』
など、測定方法を不思議に思ったり
不安を持つ方も多いですよね
そこで今回は統計学的な要素を
説明しながらワークサンプリングの
信頼度についてお話してまいります
ぜひ安心して活用いただくために
この内容をご理解ください
ワークサンプリング分析のやり方
ワークサンプリング分析のやり方は
調査対象の作業過程を予め整理して
予備調査を実施して実施計画を立てて
本調査を行って集計する方法です
詳しいやり方については
以前の説明を参考にしてみてください
[getpost id=”1342″]
複雑に感じるかもしれませんが
ようは慣れです
このワークサンプリングをやる職場と
やらない職場ではやはり管理レベルが
数段変わってきますのでぜひ
取り入れていただきたいと思います
ワークサンプリング分析の信頼度について
さてこのワークサンプリング分析では
観測する回数を決める時に活用する
計算式があります
N=観測数
S=希望する精度(相対誤差)
P=推定発生比率
実はこの計算式そのものが
すでに信頼度95%である証拠です!
なんて言っても
わけがわかりませんよね、笑
ここでこの計算式を数学的に
証明すれば説明は簡単になりますが
理解側に数学的な慣れが必要ですし
そもそもこのサイトらしくありません
そこで統計学をわかりやすく説明して
ざっくり理解いただくましょう
疑問を解くため、あるいは
ワークサンプリングを安心して
お使いいただくために
もう少しお付き合いください
統計学を応用した内容について知る
統計学にはある事象の確率を表現した
正規分布という曲線があります
ある値の発生回数のグラフで
真ん中の平均値を中心に
左右対称の曲線を描きます
これは自然界に存在する事柄は
すべてこの正規分布に当てはまると
言われている有名な曲線で
統計学の代表的な考え方です
この正規分布は大きな特性があり
この特性を応用することが
さきほどの信頼度95%を証明します
それはどんな特性か?
正規分布と標準偏差との関係
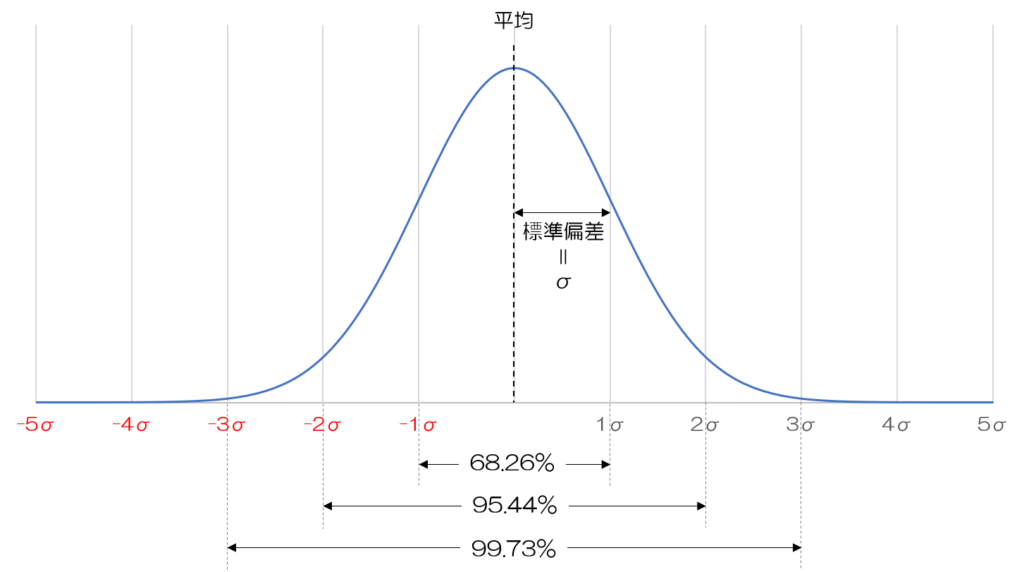
実はこの正規分布のカタチは
発生する値がバラつけばバラつくほど
横長になっていく性質があります
逆にバラツキが少なければ少ないほど
縦長になっていくわけです
そしてそのバラツキ具合を表す尺度に
標準偏差=σ(シグマ)という数値が
使われます
なんとそのバラツキを表す標準偏差と
発生確率との関係が一定だという
特性を持っているのです!
この正規分布はこの曲線の下の面積で
その事象が現れる確率を表しています
そのため平均値を挟んで左右の
±σ分の中にデータが収まる確率が
68.26%
±2σ分の中にデータが収まる確率が
95.44%
さらに±3σ分の中に収まる確率が
99.73%
となる特性を持っているのです!
正規分布と標準偏差との関係を信頼度に応用する
そんな特性をもった
正規分布と標準偏差との関係を
応用して信頼度95%を確保します
つまり
±2σ:95.44%≒95%とおいて
この特性を活用してできた計算式が
観測回数を求める式を構成していると
そういうわけなのです
4の数字が見えるのは実は
2σの2を2乗した値だったんです
ま、当たり前ですが
ちゃんと検証して作られている
計算式だっということですね
ワークサンプリング分析の信頼度とは?統計学を応用した内容を知るまとめ
信頼度95%はもちろん
100個のサンプルデータのうち
95個は真実を表し、残りの5個は
そうではないかもしれない状態です
でも、まあ一般的に言えば
信用に値する状態だと言えますねって
そういう割り切りが
前提の手法だということ
その割り切りを元にこのやり方で
稼働状態を推定的な実態を
把握してきましょうと言うのが
ワークサンプリング分析法です
いかがでしょう?少しはご納得
安心いただけたでしょうか?
それでは今日はここまでです
今後とも宜しくお付き合いください☆
長文・乱文を最後まで読んでくださり
いつもありがとうございます♪
すべては御社の発展のために
すべてはあなたの笑顔のために










